Passes Ranking 


Classification of cycling climbs and passes according to their difficulty

I present here the current methods of classification of mountain passes for cyclists according to their difficulty, then I approach the subject in a scientific way to propose a new one closer to reality.

Introduction to the classification of cycling passes:

to classify cycling passes easier than climbing the gallibier
Be brave,
it's easier to classify the Galibier than to climb it!

In cycling, the passes are classified by increasing difficulty in categories: fourth, third, second, first category and out of category. This classification is made for a long time in professional races, and allows to attribute in the ranking of the best climber, the red dot jersey in the Tour de France, a number of points to the riders who cross the first a pass or the top of a hill, depending on the difficulty of the climb and the order of passage of the runners. If it has been for a long time in a more or less empirical way, there is an attempt at rationalization, especially since the advent of the internet.

Empirical methods and square rating of passes:

When a journalist asks in 2014 the former professional rider Thierry Gouvenou, then responsible for choosing the route of the Tour de France, how he ranks a climb, he talks about the praxis: if the race has already passed by a pass in the past, most of the time he do not change his ranking. But he also does a calculation 1 : he multiplies the length of the road d by the square of his slope p, then he can change the ranking according to the position of the pass in the course; sometimes he increases the ranking of a pass placed at the end of the stage, badly felt by tired organisms. But what's interesting is the formula d.p2. Where does this thing come from? this is called the squared ranking. The formula comes from the idea that the difficulty of a climb is proportional to both its slope p and its height difference h. As h=p.d, we get well d.p2. Guy Bodoin presents in detail this method in his climbs study 2: it complicates the calculation by dividing the rise in parts then adding the score of each of them, which seems good to him when the ascent is irregular.

ranking of the cycling passes by the quotation with the squared ranking

Bodoin asserts, however, that his calculations are only relevant for the hardest climbs, those with a result of at least 750.
Someone suggested 3 to modify the formula by adding the distance d to the result, which gives d.p2+d = d.(1+p2), and names the result "ranking squared of the mean". A scientist will not fail to notice that a formula is proposed without really justifying it, then modified to have a result that looks more or less good. The first problem is the assumption that the difficulty would be proportional to the slope and the vertical drop. This is not really clear because in the physical sciences the difficulty of the runner's action is equal to the work of the force he provides during his ascent, or by its power as instant characteristic. Assume that this work or this power could be formulated in the form d.p2, is supposing the result of a calculation without doing it. A result provided without any demonstration is a matter of magical thinking. Especially when it can be shown that this formula does not correspond to a work, a power, or anything mechanical. Note also that this formula has the unit of a distance, therefore neither that of a work, nor of a power. It is simply an error due to a lack of scientific rigor.

Enough pseudo-scientific do-it-yourself, let's go on to the physical reality of the cyclist climbing a pass:

Let's look at the problem as a physician. I will show you how to classify the passes in a rigorous way. So now here are some explanations on how I do this ranking, in the most scientific way possible, taking into account their real difficulty for cyclists, and demonstrating my results.

Consider a cyclist riding an ascent with a constant slope p. He travels a distance d and increases his altitude by the value h: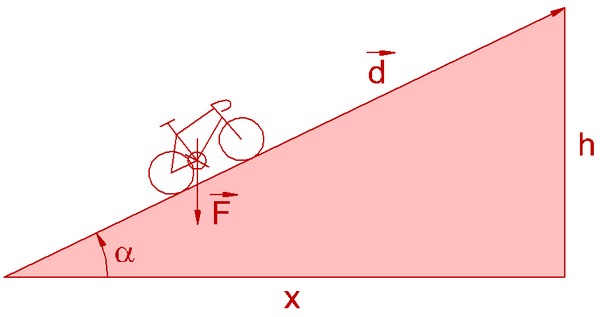

schema of the mechanical study of the efforts and the cylist power to climb a pass

To ride, the cyclist provides a power P during a time t. The difficulty of the climb, for him, is to be able to provide this power during all this time: it is proportional to P, but also to t. The difficulty of the pass is therefore proportional to P.t. This value P.t is what physics defines as the work of the force that the cyclist provides to advance.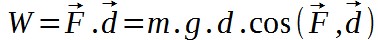
In a pass, the greatest force the cyclist has to overcome is the gravity, represented by F on the diagram. The air resistance is low; I know that riding a pass with a a wind from the front can be very hard, but you will agree that it does not come from the pass itself (ah, if we could the Ventoux under a dome!). Nor is friction taken into account, and the rolling resistance due to the contact of the tires on the ground.
The difficulty of the pass comes from the fact that the cyclist must provide a work superior to that which the gravity deploys from the beginning to the end of the ascent. The value of this gravitational force F is m.g, where m is the mass of the cyclist with his bike, and g the constant of earth gravity.
The work that gravity will provide to prevent the cyclist from riding is:

Let us represent the angle we are talking about the cosine: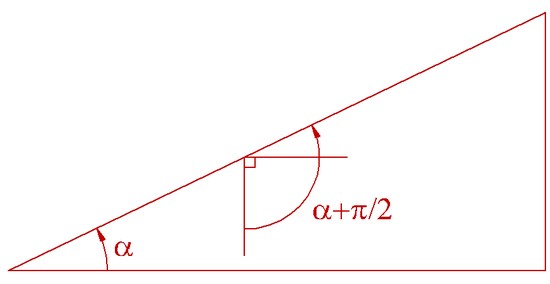

diagram of the angle between the cyclist's weight and his displacement by climbing a pass

Therefore:

By simplifying we get: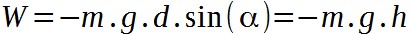

Conclusion: only three parameters are in the expression of the difficulty that the cyclist must face: its mass, the gravity and the difference in altitude. Mass and gravity do not depend on the topography of the pass; the only parameter in dependence is the elevation h. The negative sign means that it is a challenge to overcome by providing more positive work.

The physical difficulty of a pass is proportional to its height difference.

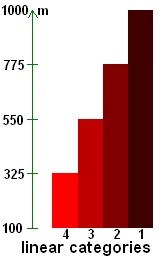
Note: this result is not surprising, since m.g.h is also the potential energy gained by the rider and his machine by mounting the pass.

Proposed definition of cycling pass categories according to their difficulty:

Taking into account what has just been demonstrated, I propose to define the categories of passes by taking into account only their altitude difference. I place the start of the passes out of category to a vertical drop of 1000 meters; this allows to correctly classify the Izoard, one of the hardest out of category passes, and Peyresourde, a very hard first category pass.

I propose to place the beginning of the fourth category at a height of 100 meters, to not include almost flat roads.

For categories 1, 2, 3 and 4, I propose to divide the interval from 100 to 1000 meters into four intervals, equal for the moment, which will correspond to the categories. Each of these categories will thus include an interval of 225 meters of altitude difference. This will give:

CategoryHeight difference
4100 to 325 meters
3325 to 550 meters
2550 to 775 meters
1775 to 1000 meters
Out of category1000 meters or more
ranking of cycling passes in linear categories

Note: the lower bounds are included in the range, upper bounds are excluded.

However, the use of these intervals showed me that they are not good because their width, strictly equal, does not correspond to the physiology of the cyclist. Indeed, when it climbs for example 800 meters, the difficulty he feels in the second half, to climb from 400 to 800 meters above the starting altitude, is not the same as he felt in the first half, from 0 to 400 meters. Going away fresh and available at the meter zero he is, arrived at half of the coast, after 400 meters, significantly more tired, because he already has 400 meters "in the legs"... It is this cumulative effect that makes a c-category climb more difficult than a c-1 category, the next lower category. The difference between two categories is not just a matter of time, because man is not a machine. It's not directly because it takes longer than it is more difficult, it is because we are more tired and this fatigue accumulates (partially, everything depends on the specific muscular mechanisms at play depending on the characteristics of the cyclist and how he manages his effort by pressing more or less on the pedals).
This is why the best adapted scale to represent the difficulty of a climb for a cyclist is not linear. To take into account the accumulation of fatigue, logarithmic scales are used in exercise physiology. I propose to approach the classification of passes as a study combining physical sciences and exercise physiology, by setting the boundaries of the categories using a logarithmic scale.
In a linear scale, the widths of the intervals are identical; with a logarithmic scale too, after passing through logarithmic.
With the values 100 and 1000 meters, calculations are easy with 10 logarithms because log10(1000)=3 and log10(100)=2.
The log10 limit logs are 2 then 2.25 then 2.5 then 2.75 and finally 3, because they are regularly spaced from log10(100) to log10(1000), and the limits are 102, 102,25, 102,5, 102,75 and 103 meters.
All calculations done, thus keeping 100 meters as plane limit and 1000 meters as out-of-category limit, we obtain the following intervals:

CategoryHeight difference
4100 to 178 meters
3178 to 316 meters
2316 to 562 meters
1562 to 1000 meters
Out of category1000 meters or more
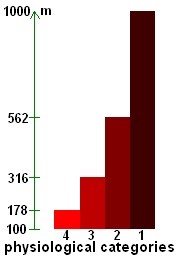
classement des cols cyclistes en categories physiologiques

These are the intervals I propose for final adoption. Simulations with the power calculation software that I developed (see this dedicated page) have shown that, in most cases, with these intervals, I obtain identical results as in professional cycling races.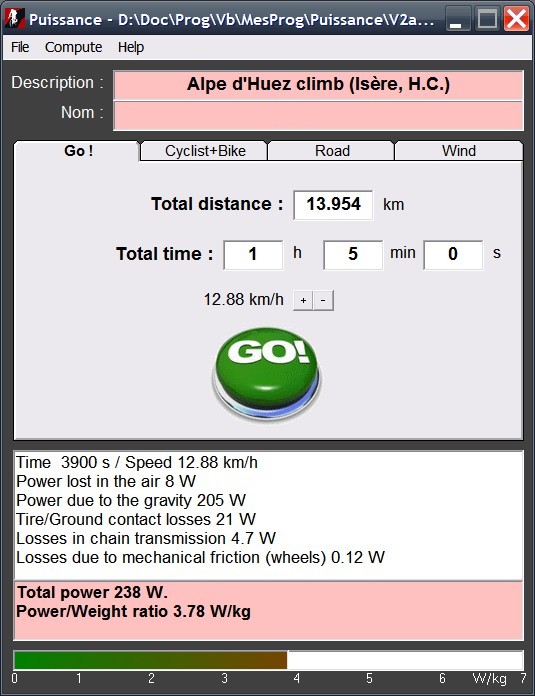
Here is for example the information that my sotware gives for the Alpe d'Huez:

ranking of the alpe d'huez by the quotation on the square, on the square of the average, and by the denivele

Notes and references

1.Sylvain Mouillard, Comment les cols du Tour de France sont-ils classés ?, liberation.fr, 2014.

Comments

There is no comment yet. Be the first to write one!

Write a new comment ..